1. 이진수. Boolean 배열/벡터.
<ㅡㅡㅡㅡㅡㅡㅡㅡㅡ
128 64 32 16 8 4 2 1
1 0 1 1 0 0 0 0(176)
| 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
2. 비트 연산자
| & | 비트단위로 AND 연산 |
| | | 비트단위로 OR 연산 |
| ^ | 비트단위로 XOR 연산(같으면 0, 다르면 1) |
| ~ | 피연산자의 모든 비트 반전 |
| << | 피연산자의 비트 열을 왼쪽으로 이동 |
| >> | 피연산자의 비트 열을 오른쪽으로 이동 |
* 10진수 -> 2진수 변환 사이트
Decimal to Binary Converter
Divide by the base 2 to get the digits from the remainders: Divisionby 2 Quotient Remainder(Digit) Bit #
www.rapidtables.com
* 비트 연산 공식
a >> b = (int) a * (1/2)^b
a << b = a * 2^b
3. 비트의 음수표현
: 비트 반전 하고 +1 한 값
*비트 음수연산 공식
~a = -(a + 1)
ex) 0001000(8) 음수만들기: 0001000 --(비트반전)--> 1110111 --(1더하기)--> 1111000(120)
4. 비트 연산자 활용법
| idx 번째 비트끄기 | S &= ~(1 << idx) |
| idx 번째 비트 XOR 연산 | S ^= ~(1 << idx) |
| 최하위 켜져있는 비트 찾기 | idx = (S & -S) |
| 크기가 n 인 집합의 모든 비트 켜기 | (1 << n) - 1 |
| idx 번째 비트켜기 | S |= (1 << idx) |
| idx 번째 비트가 켜져 있는지 확인하기 | if(S & (1 << idx)) |
1) idx 번째 비트끄기
ex. 10010 의 1번째 비트끄기.
10010 & ~(1 << 1) = 10010 & ~(10) = 10010 & 01 = 10000
2) idx 번째 비트를 XOR 연산자 취하기
ex. 10010 의 0번째 비트가 1이면 0, 0이면 1로 바꾸기(XOR 연산)
10010 ^ ~(1 << 1) = 10010 ^ ~(10) = 10010 ^ 01 = 10011
3) 최하위 켜져있는 비트 찾기
cf. 최하위 비트: 10010 이면 1번째 1, 10001 이면 0번째 1.
cf. ~S = -(S+1)
ex. 10010 에서 최하위 켜져 있는 비트 찾기.
10010 & -10010 = 10010 & (~10010 + 1) = 10010 & (01101 + 1) = 10010 & 01110 = 00010
4) 크기가 n인 집합의 모든 비트켜기
ex. n이 4인 모든 비트켜기.
(1 << 4) - 1 = 10000 - 1 = 1111
ex. n이 5인 모든 비트켜기.
(1 << 5) - 1 = 100000 - 1 = 11111
5) idx 번째 비트켜기
ex. 10010 의 0번째 비트켜기.
10010 | (1 << 0) = 10010 | (00001) = 10011
6) idx 번째 비트가 켜져 있는지 확인하기
ex. 10010 의 3번째 비트가 켜져있는지 확인하기
if(10010 & (1 << 3)) = if(10010 & 1000) = if(00000) = 0 = 꺼져 있음.
ex. 10010 의 1번째 비트가 켜져있는지 확인하기
if(10010 & (1 << 1)) = if(10010 & 10) = if(00010) = 1 = 켜져 있음.
5. 비트마스킹, 경우의 수, 매개변수
*비트마스킹
: boolean 배열 역할을 하는 하나의 숫자를 만들어서 비트 연산자를 통해 탐색, 수정 등의 작업을 수행하는 것.
*비트마스킹을 이용한 경우의 수
Q. {사과, 딸기, 포도, 배} 의 모든 경우의 수 구하기.
A. 총 16가지 경우의 수. (포함하거나 포함하지 않거나의 경우의 수로 2^4 = 16가지가 나옴)
#include <iostream>
using namespace std;
const int FRUITS_NUM = 4;
int main(){
string fruits[FRUITS_NUM] = {"사과", "딸기", "포도", "배"};
for(int i = 0; i < (1 << FRUITS_NUM); i++){ // 0000(0) ~ 1111(15) 까지 경우의 수 구하기(10000 보다 작은)
string result = "";
for(int j = 0; j < FRUITS_NUM; j++){ // 0 ~ 3 자리를 돌면서 켜져 있는 비트 찾기
if(i & (1 << j)){ // 켜져 있니 ~?
result += (fruits[j] + " ");
}
}
cout << result << '\n';
}
return 0;
}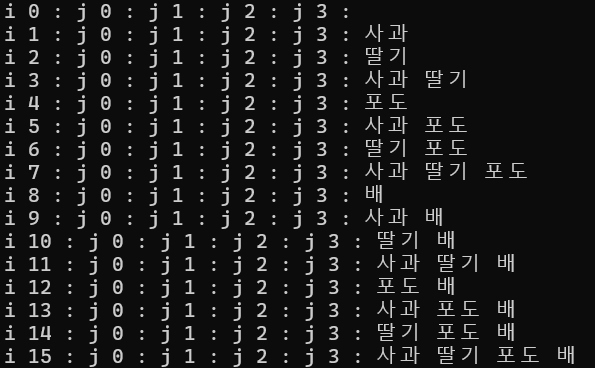
: 비트마스킹 0 1 로 모든 경우의 수를 체크하며 경우의 수를 구한다.
바깥 for문 i
0 ~ 1111(10000보다 작을 때 까지) 까지 수 늘리기. (0~15. 16가지 경우의 수)
안쪽 for문 j
0 ~ 3 자리를 돌며(4보다 작을 때 까지) 현재 자리가 켜져 있는지 확인하기
0 & (1 << 0) = 0000
0 & (1 << 1) = 0000
0 & (1 << 2) = 0000
0 & (1 << 3) = 0000
1 & (1 << 0) = 0001 & 0001 = 0001 사과
1 & (1 << 1) = 0001 & 0010 = 0000
1 & (1 << 2) = 0001 & 0100 = 0000
1 & (1 << 3) = 0001 & 1000 = 0000
2 & (1 << 0) = 0010 & 0001 = 0000
2 & (1 << 1) = 0010 & 0010 = 0010 딸기
2 & (1 << 2) = 0010 & 0100 = 0000
2 & (1 << 3) = 0010 & 1000 = 0000
3 & (1 << 0) = 0011 & 0001 = 0001 사과
3 & (1 << 1) = 0011 & 0010 = 0010 딸기
3 & (1 << 2) = 0011 & 0100 = 0000
3 & (1 << 3) = 0011 & 1000 = 0000
4 & (1 << 0) = 0100 & 0001 = 0000
4 & (1 << 1) = 0100 & 0010 = 0000
4 & (1 << 2) = 0100 & 0100 = 0100 포도
4 & (1 << 3) = 0100 & 1000 = 0000
5 & (1 << 0) = 0101 & 0001 = 0001 사과
5 & (1 << 1) = 0101 & 0010 = 0000
5 & (1 << 2) = 0101 & 0100 = 0100 포도
5 & (1 << 3) = 0101 & 1000 = 0000
6 & (1 << 0) = 0110 & 0001 = 0000
6 & (1 << 1) = 0110 & 0010 = 0010 딸기
6 & (1 << 2) = 0110 & 0100 = 0100 포도
6 & (1 << 3) = 0110 & 1000 = 0000
7 & (1 << 0) = 0111 & 0001 = 0001 사과
7 & (1 << 1) = 0111 & 0010 = 0010 딸기
7 & (1 << 2) = 0111 & 0100 = 0100 포도
7 & (1 << 3) = 0111 & 1000 = 0000
8 & (1 << 0) = 1000 & 0001 = 0000
8 & (1 << 1) = 1000 & 0010 = 0000
8 & (1 << 2) = 1000 & 0100 = 0000
8 & (1 << 3) = 1000 & 1000 = 1000 배
...
15 & (1 << 0) = 1111 & 0001 = 0001 사과
15 & (1 << 1) = 1111 & 0010 = 0010 딸기
15 & (1 << 2) = 1111 & 0100 = 0100 포도
15 & (1 << 3) = 1111 & 1000 = 1000 배
'📝 Coding Test Study > C++' 카테고리의 다른 글
| ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); (0) | 2024.04.15 |
|---|---|
| 문자열 ASCII code 값 (0) | 2024.02.17 |
| [10주 완성 C++ 코딩테스트] 누적합, Prefix Sum (0) | 2023.08.11 |
| [10주 완성 C++ 코딩테스트] 필수개념 - map, unique() (0) | 2023.08.06 |
| [10주 완성 C++ 코딩테스트] 필수개념 - 메모리와 포인터(pointer) (0) | 2023.08.05 |